The Sound of the Machine
The Hidden Harmonics behind THD
The deepest challenge of designing high fidelity equipment is finding the common ground between truth and beauty, left brain/right brain, or more plainly, reconciling the interior experience of listening with the technical world of measurements. If you can’t reconcile the two, or insist that only one exists, you are flying blind. Since I’ve been designing speaker systems for the last twenty years, I’ve spent much of that time finding associations between the perceptual experience and measurements. With so many possible analytic techniques (frequency response, group delay variation, inter-driver phase angle, polar response vs frequency, cumulative waterfall display, IM distortion vs frequency, etc), the hard part is deciding which set of measurements are the most significant.
The contention that occurs in speaker-design circles is the result of many different arguments over which measurements are the most important. No speaker can possibly "do it all" — designers are forced to choose which parameters are the most important, and let others slide. That’s why speakers at all price points sound so different; they have been optimized by the designer for different characteristics, and the marketing campaign based on the hip philosophy of the moment. Today, it’s high efficiency; yesterday, minimal crossovers; before that, linear phase, further back, low coloration, and way way back in the prehistory of the hi-fi business, the West Coast vs East Coast Sound. You get the idea!
With electronics, it all seems so much simpler; no worries about polar response, transient response is superb compared to speakers, and just about any amplifier is flatter and more wide-band than the best transducers - microphones, headphones, or speakers. So what’s to worry about? Just measure the distortion, and there you are.
Unfortunately, it’s not that simple. In electronics, the subjective correlation between Total Harmonic Distortion (THD) and what you actually hear is close to zero. After all, a low-fi rack-stereo receiver has far lower THD than the best-regarded triode amplifier. Does that mean that "all amplifiers sound the same?" No, certainly not with high-performance speakers. Is the converse true — that measurements are meaningless? No, that’s not true either; there are plenty of amplifiers with terrible measurements that do indeed sound terrible.
The fault is not with the subjective perception of the listener, but rather in the measurement itself. Nothing new in that; you can measure all you want, but a mass spectrometer isn’t going to find a lot of difference between lunch at a high school cafeteria and the best dinner at a four-star restaurant. To foolishly assert that the mass-spectrometer is right, and the restaurant customers are all deluding themselves with some kind of "placebo effect," is an example of simple ignorance trying to cover its nakedness with the fig-leaf of Science.
The restaurant customer — or dedicated hi-fi enthusiast — have been right all along in their subjective perceptions; it’s up to the serious designer to find out what’s going on beneath the surface, and not indulge in vague pseudo-scientific hand-waving about "euphonic distortion" and "placebo effect." All we can say for certain right now is that simple THD figures are not the right measurement for electronics!
When Matt Kamna (my Tektronix colleague) offered to test several vacuum-tube driver circuits with his HP 3585A spectrum analyzer, I jumped at the chance. I’ve been curious for a long time about finding out why different circuits sound the way they do. Circuit changes in amplifiers can sound exactly like a 1 to 2dB crossover change in a speaker, yet the circuit change will have no effect on the measured frequency response of the amplifier!
What made this interesting is that the HP 3585A has an exceptional 100dB on-screen dynamic range, and measures out to 40 MHz. (Just the thing for cleaning up noisy DAC’s and CD players.) To extend the dynamic range even further, Matt used the "distortion out" port of a Tektronix AA501A distortion analyzer feed the input of the HP 3585A. By using the AA501A to reject the fundamental tone before it reached the HP, we gained another 20 dB, yielding a total measurement range of 0 dB to -118 dB.
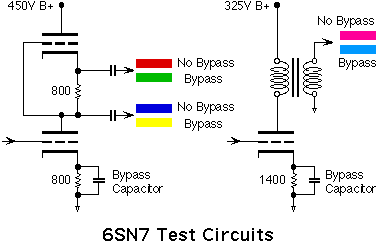
To simplify the analysis, we chose a 1kHz sinewave and adjusted the drive level to produce a constant output level of 50V rms. If the test frequency were any higher, the upper harmonics might look a little better than they actually were due to circuit rolloffs. I also wanted the important 2nd, 3rd, 4th, and 5th harmonics to fall in the 1 to 5kHz region, where the ear is most sensitive to distortion.
The choice of 50V rms output level was arbitrary, but represents a good compromise between 300B, 2A3, and EL34/KT88 drive requirements. With a 50V rms output level, the noise floor of the instrumentation is 118dB down from the fundamental signal, resolving down to 0.0002% distortion.

The same NOS 6SN7 dual triode was used for all seven test circuits. (The 7th circuit, not shown, was a conventional 2-stage RC-coupled cascade.) The 6SN7, first designed in 1940, is still one of the most linear driver tubes, with distortion typically several times lower than 12AU7’s and 6DJ8’s. To get distortion much lower than a 6SN7, you have to pick antiques like 76’s, 56’s, and a real old-timer, the direct-heated 26. I’ll leave those distortion tests to "Vacuum Tube Valley" magazine!
(Note: I realize not everyone has an exotic setup like a Tek SG505, Tek AA501A, and a HP 3585A. All of these measurements could be repeated with a test setup as simple as a good test CD (set to Repeat) and a PC-based FFT analyzer. To get wide range distortion measurements, it would be useful to construct a passive LC notch filter to remove the 1kHz fundamental from the output of the circuit under test. In effect, that’s all the AA501A was doing, rejecting the 1kHz fundamental, and improving the on-screen resolution of the HP 3585A analyzer.)
Once we got the test set-up up and running, we could certainly see a lot of fine detail, but as usual, the spectrum analyzer display was difficult to interpret, with 3rd, 4th, 5th, etc. harmonic levels bouncing up and down all over the place. It wasn’t obvious to see how any of these circuits was creating a particular harmonic "signature." I thought about the problem for a while, and realized that all of the even harmonics are created by asymmetric distortion mechanisms, and all of the odd harmonics are created by symmetric distortion mechanisms. All Matt and I had to do was write down each of the harmonics in -dB levels, separate out the evens and odds, and plot them out. Rather than do all this tedious plotting by hand, I used Microsoft Excel(tm) to do the plotting.
Interpreting the Data
After a bit of Excel charting, the hidden patterns became evident. Since the evens and odds are rolling off at different rates, when you look at the raw spectrum analyzer display, all you see is a ragged sawtooth pattern. Interleaved within this sawtooth pattern are pairs of of distortion curves, one for the even harmonics, and one for odd harmonics. These two sets of curves have very different effects on IM sidebands.
Even (asymmetric) harmonics create distant sidebands, while odd (symmetric) harmonics create close-in sidebands. Think of the spectrum of a CCIF 14 + 15kHz test-tone and the picture gets a bit clearer. The waveform looks a bit like an AM signal, with a "carrier" at 1 kHz. If you clip off only the tops of this waveform (asymmetric, even harmonic distortion), you get sum-and-difference tones at 1 and 29 kHz. If you clip off the tops and bottoms of the waveform (symmetric, odd harmonic distortion), you get sum-and-difference tones at 13 and 16 kHz.
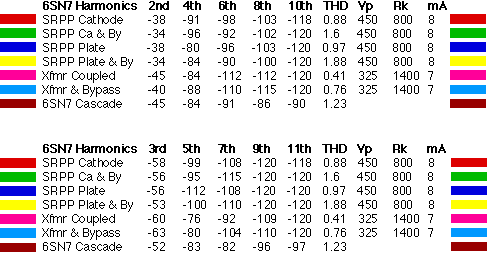
Looking at the data and graphs, note how the raw THD number is almost entirely dominated by 2nd harmonic; the danger of relying on the traditional THD "spec" is that it ignores all of the complex behaviour of the upper harmonics, and their pattern of fall-off. The quite different behaviour of the upper harmonics is hidden by similar-looking THD figures.
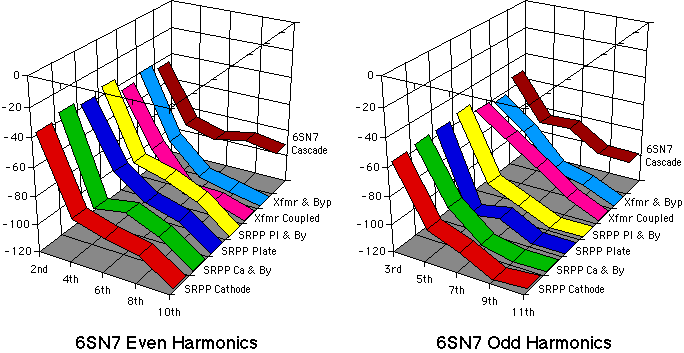
Some 6SN7 circuits show signs of harmonic cancellation at certain harmonics and not others, while other circuits have a smooth "textbook" falloff of harmonics. Harmonic cancellation in a circuit that is almost but not quite push-pull (SeRies Push Pull) can be level dependent, with nulls moving around depending on where the two curves of the triodes intersect. In other words, don't count on cancellation effects to be predictable unless great trouble is taken to maintain dynamic balance over a wide range of signal levels.
This, perhaps, is the reason for the subjective tonal balance of various circuits that does not show up on any frequency response curves. What the listener may be hearing is a spectral tilting of the noise and distortion floor of the circuit, which subjectively sounds like a frequency-response problem — but isn’t. Some of the subjective perception of spectral balance may indeed have more to do with noise-floor tilting and upper/lower harmonic patterns than actual frequency response deviations. Most of us have heard tinny-sounding transistor amps, or dull-sounding "vintage" amps — they measure flat, but they sure don’t sound that way!
A change as small as disconnecting a cathode bypass capacitor alters the upper-harmonic spectrum. Although this might seem like a trivial change, it considerably changes the operating characteristics of the triode. If a triode is used with fixed bias or a bypass cap, the specifications in the tube manual for mu, dynamic plate resistance (Rp), and transconductance (gm) are a reliable guide for design. When the bypass cap is omitted, Rp and gm both change — and by a considerable amount.
The "common wisdom" is that when you intentionally omit the bypass cap, it adds local feedback, linearizing the circuit. This is true, but is really only part of the story. What also happens is that while mu stays the same, the dynamic plate resistance goes way up, and the transconductance goes way down. For example, for a 6SN7 with 800 ohms of cathode resistance, the Rp goes from 7700 ohms up to 23,700 ohms — an increase of more than three times! The transconductance is also cut to one-third of the previous value. In effect, the performance of the tube is greatly degraded — exactly the same effect as a large drop in emission.
In terms of RC-coupling, there are severe consequences for not bypassing the cathode. To achieve low distortion, triodes like to see a load impedance no less than three to four times higher than the dynamic plate resistance of the tube. Since the load with RC-coupling is set by the fixed plate resistor in parallel with the grid-resistor of the following stage, there is little scope for increasing the load resistance except by increasing the B+, which creates problems elsewhere in the amplifier.
When the bypass capacitor is removed, the previously satisfactory Rp /Plate Load ratio becomes much less favorable, since the effective Rp is now three times higher. True, there is local feedback to help overcome this. But the tube itself is now driving a load that effectively looks much lower than it did before, rotating the load-line closer to the vertical, and resulting in signal swings into the very nonlinear low-current region.
This has consequences for the resulting distortion spectrum. The tube now has intrinsically higher distortion (unless it is transformer or mu-follower coupled), which is partly masked by local feedback. This will result in lower 2nd harmonic, but upper harmonics may well be worse due to the less favorable load-line seen by the plate.
In the data shown here, the effect is not obvious, but then again, Matt and I avoided RC-coupling except for the conventional 2-stage cascade circuit, which does indeed have higher upper harmonic content. Although we didn’t measure it, if the conventional circuit had unbypassed cathodes, it might be even worse. The circuits that avoid standard plate-load resistors come out pretty well in comparison.
The smooth fall-off of harmonics is especially noteworthy in the transformer-coupled circuit - the reason for the excitement about the naturalness and "directness" of transformer coupling is obvious when looking at the spectral data. This is the best distribution of harmonics I've seen — looking almost exactly like an RCA "textbook" distribution of spectral content. The overall magnitude of the distortion is impressively low as well — try and find a transistor circuit that can deliver 50V rms at less than 1% distortion with no feedback!
The Sound of Different Harmonic Spectra
As mentioned above, odd and even harmonics can be recast as asymmetric distortion and symmetric distortion, thus the very different effects seen with IM distortion tests. As D.E.L. Shorter of the BBC pointed out in the April 1950 Issue of Electrical Engineering, real music is dominated by a great many closely-spaced tones - a choir or massed violins having the most dense spectra of all. Shorter showed that with a few as three closely spaced tones, IM sum-and-difference sidebands outnumber the much simpler harmonic series. In effect, as the number of tones increase, the number of IM sidebands increase at much faster rate than simple harmonics. The boundary case is 3 tones of equal magnitude; for 2 tones, IM is about the same as harmonic distortion, for 4 tones, IM is far greater than harmonic distortion. I leave it to the imagination of the reader to figure out how many simultaneous tones are present in real music — a lot more than three!
The influence of IM vs THD has additional consequences for the type of music we listen to. Jazz and folk music have sparse spectra, thus THD will play a larger role in subjective coloration. By contrast, a cappela singers, large choirs, and massed violins have very dense spectra, with many closely-spaced tones drifting in and out of phase-lock all the time. This type of music will be strongly degraded by even small amounts of IM, but not as sensitive to relatively small amounts of low-order harmonic distortion. Thus the origin of the endless audiophile wrangles that are actually based on the type of music the listener prefers.
(Musicians can and do maintain phase-lock for a few seconds, despite the seeming impossibility of this. I found that out the hard way on my work on the Audionics Shadow Vector quad decoder. Every now and then on certain records the dynamic matrix circuits would go crazy — this turned out to be brief periods of phase-lock by the musicians. The SQ-encoded Loggins & Messina "Full Sail" album had one track with a violin in Left Back, and a harmonica in Right Back. Sounded great in stereo and on headphones, but with quad decoding, the logic detector would whirl the sound round the room as the musicians drifted in and out of phase-lock. Truly weird effect, and not apparently intended by the producer.)
So, depending on the type of music you listen to, the spectral distribution and class of distortion (symmetric vs asymmetric) will affect the subjective tonal character. It is much more complex than the simplistic "2nd Harmonic is Always Better" guff reprinted in the popular press.
Preference for spectral distribution plays a major role in the "tone color" of an otherwise flat-response amplifier. Thinking about "spectral tone color" in a more sophisticated way shows just how far off-course we have drifted in The Age of Digital.
The Effects of Feedback on Harmonic Structure
The Williamson amplifier of 1947 was the design that did the most to popularise the "feedback cures all ills" philosophy. It is interesting during the period from 1948 to 1956, almost all commercial hi-fi amplifiers were Williamson topologies (with minor exceptions for Quad II, McIntosh, and EV Circlotron). During this formative period the mantra of "more power, lower THD" became the driving force in the industry. By 1960, ultra-wide bandwidth, heavy feedback, and Class AB EL34 and 6550 UL circuits ruled the industry.
In the span of twelve years, the traditional audio-engineering prejudice against high-distortion devices faded, opening the door to high-power pentodes and Class AB operation. Each "improvement" was characterized by an increase in device distortion, which was then "corrected" by more and more feedback. Transistors circuits with even higher feedback ratios were the next obvious step - after all, they had more power, lower THD, more bandwidth, and most important of all, cost less to build.
Norman Crowhurst wrote a fascinating analysis of feedback multiplying the order of harmonics, which has been reprinted in "Glass Audio," Vol 7-6, pp. 20 through 30. He starts with one tube generating only 2nd harmonic, adds a second tube in series (resulting in 2nd, 3rd, and 4th), and then makes the whole thing push-pull (resulting in 3rd, 5th, 7th, and 9th), and last but not least, adds feedback to the circuit, which creates a series of harmonics out to the 81st. All of this complexity from "ideal" tubes that only create 2nd harmonic!
With real devices there are even more harmonics. In terms of IM, actual amplifiers have complex and dynamic noise floors thanks to the hundreds of sum-and-difference IM terms. That's not even counting the effects of reactive loads, which adds a frequency dependency to the harmonic structure! (With reactive loads, additional harmonics appear due to the elliptical loadline seen by the power tubes. The elliptical load-line dips into the very nonlinear low-current region, resulting in an instantaneous increase in upper harmonics. This spectral "roughening" is most audible with strong low frequency program material and hard-to-drive horn or vented bass drivers.)
As Crowhurst noted, feedback mostly reduces the 2nd and 3rd harmonics, leaving the upper ones more or less alone, or sometimes even greater than before. Feedback fools the simple THD meter, but the spectrum analyzer sees through the shell game. Too bad raw power and almost useless THD measurements became the end-all and be-all for more than 50 years. If more engineers and reviewers had access to spectrum analyzers, the misleading nature of raw THD measurements would have been discovered earlier, and amplifier design might have taken a different course.
If device-level linearity and absence of high-order harmonics become your goal, then direct-heated triodes are the only way to go - they have about 1/3 the distortion of triode-connected pentodes and beam tetrodes. The spectral distribution is better as well. Seen in this context the Sakuma amps with their 300B direct-heated driver tubes start to make sense - with a 300B swinging 65V rms into a high-impedance transformer load, the driver will have very low distortion, maybe as low as 0.1% for push-pull drivers.
For once, the driver tube would be out of the picture as far as distortion is concerned — and this is much more rare than you would think. Very few amplifiers have driver sections with distortion 1/3 of the output stage and 5 dB or more of headroom — this is true for triode, pentode, or transistor amps as well! Much more typical is 1/2 or more distortion compared to the output, and 1 to 2 dB of headroom. As a result, 2A3 and 300B amps all sound different, depending on the linearity and current delivery of the driver circuit.
Device, Topology, and Harmonic Spectra
All of the foregoing applies to triodes — conventional RC-coupled, transformer, choke-loaded, SRPP, and active-load circuits such as mu-followers. It does not apply to: cascode-connected triodes, pentode, bipolar transistor, or MOSFET’s. This second group of devices do not have the simple square-law transfer characteristic of triodes; instead they have a much more complex exponential curve, and that translates into a much greater proportion of upper harmonics.
When you compare device specifications, take a close look at the ratio of 2nd to 3rd harmonic distortion for a basic single-ended circuit. Low-distortion triodes (6J5, 6C5, 6SN7, 6CG7, the new JJ ECC99, and direct-heated types) have much lower 3rd harmonic; for devices in the second group, the 3rd harmonic will equal or exceed the 2nd harmonic. Medium-to-high distortion triodes (12AU7, 6DJ8) fall between the two groups. (This is why the 6DJ8 is known for a "high-definition" transistor-like sound - the distortion spectra isn’t that different!)
Sometimes people get a little confused at the differences and similarities of SRPP, mu-followers, cascode, and pentode. The important distinction is to find what’s driving the upper grid, which behaves in the same way as the screen grid in a pentode. At audio frequencies, if the upper grid tracks the voltage swing on the lower plate, the composite device will behave like a triode. If the upper grid is AC-coupled to ground, then the composite device will behave like a pentode (or beam tetrode). If the upper (or screen) grid is connected to small fraction of the voltage swing, this is called ultra-linear operation, with distortion characteristic partway between triode and pentode operation.
Triode operation is characterized by a low plate resistance (Rp), low to moderate gain (mu), medium to high Miller capacitance, and low distortion with rapid falloff of upper harmonics. Comparisons of triodes to other classes of device reveals that they have lowest distortion of any amplifying device ever made.
Pentode (or cascode) operation is characterized by very high plate resistance, medium to very high gain (depending on the impedance of the load), very low Miller capacitance, and medium to high distortion with a large proportion of upper harmonics. From this it can be seen that pentodes (or cascodes) are best suited for very low-level amplification and RF frequencies, where distortion is less important than noise and high-frequency amplification.
With the advent of Class A transistor amps, followed by the vacuum-tube revival in the late Eighties (thank you, Glass Audio), device linearity is once again starting to be seen as important, especially with the revival of direct-heated triode amplifiers. What has gone unnoticed in the uproar over so-called "high-distortion" SE direct-heated triode amplifiers is that the output-tube distortion is actually 3 times lower than the next-best devices, triode-connected pentodes. (Don’t think so? Read "Vacuum Tube Valley" magazine, which shows just this result for 300B’s, 6L6’s, EL34’s, and 6550’s.)
With power devices, you don’t get much choice about loading; to deliver power into the speaker, you must use a transformer, and all that does is translate volts into amps. Any attempt to raise the load impedance seen by the power tube plate inevitably decreases power, so most triode amplifier designers choose primary impedances between 3 and 6 times the Rp of the power tube. This gives a reasonable compromise of power, low distortion, and adequate damping factor for the speaker. (The damping factor seen by the speaker is close to the ratio between Rp and the primary impedance.)
For driver circuits, there are the options of active loads (mu-follower), transformer coupling (providing very high impedances in the audio range), or direct-coupling to the power-tube grid (assuming bias-stability problems can be dealt with). Triodes and pentode/cascode/transistor circuits have very different responses to increased load impedances.
For triodes, there is a moderate increase in gain, a large decrease in distortion, and the possibility of even greater decreases in upper-harmonic distortion. In effect, if the load impedance is an impedance 10 or more times the Rp of the driver tube, the triode can be persuaded to behave as a near-ideal triode. (In practice, distortion in the mu-follower can interact with the distortion in the driver tube, resulting in a more complex transfer curve.)
For pentodes, cascodes, and transistor drivers, raising the load impedance results in very high gain, a possible increase in distortion, and a possible increase in upper-harmonic content. This is a very different picture than triodes; however, if the amplifier has feedback, the increased gain can be used to increase the feedback factor. The increase in feedback greatly reduces the lower harmonics (2nd and 3rd), but as mentioned earlier in the Crowhurst article, does nothing to reduce the upper harmonics. Increased feedback also leads to sharper clipping, which decreases the subjective sense of dynamic range.
So if you were to compare 2 transformer-coupled low-mu triodes to a single pentode or a transistor with active loads, the overall gain and raw THD might be similar, but the proportion of upper harmonics will almost certainly be much greater with the high-gain, high-feedback circuit. The old Brook ads are right: low-mu triodes throughout are the way to go, even if it takes a few more devices to do the job.
Power Supplies and Noise Spectra
The electro-magnetic interference (EMI) noise generated by bridge-capacitor and pi-filter power supplies is responsible for a significant amount of tonal coloration as well as low-level veiling.
The first power-supply cap connected directly to the rectifier charges up very rapidly — the caps are "topped up" by a brief but very powerful spike of current. (Refer to Chapter 30 in the RCA Radiotron Designers Handbook, Fourth Edition, Fig. 30.1 for a more complete discussion of peak current flow in pi-filter supplies).
What goes unnoticed by most readers is the pulse-width of this brief current spike is in turn modulated by the moment-to-moment current draw of the amplifier. If the current demand is heavy, the spike is wider, and if the draw is low, the spike is narrower. Jumping to the frequency domain, the wider spike will have stronger low-frequency components, and the narrower spike will have more high-frequency components ... although both spikes yield a comb spectra going out to at least 100 kHz or more, depending on the residual inductance of the first power-supply capacitor. In effect the noise spectrum of the power transformer secondary/rectifier/cap antenna is modulated by the current draw on the entire amplifier.
If you recast the bridge-capacitor & pi-filter supplies as a Tesla coil (inductor, commutator, cap) the picture gets clearer. The EMI spectrum of this miniature RF transmitter is pulse-width-modulated by the inverse of the current draw.
This isn't so bad for true, all-the-time, Class A circuits, since the current demand is theoretically constant; for more common Class AB circuits, though, it is a disaster. The current demand for Class AB fluctuates a great deal, especially for transistor amplifiers that typically idle at a few watts. This means the noise spectra of the power supply (which extends into RFI frequencies) is always changing with the music.
This might be the single greatest advantage of choke-fed supplies; at least the current pulse through the rectifier is much wider and not significantly affected by current demand. It also looks like folks who are stuck with bridge-capacitor supplies (the worst kind) for heater supplies and solid-state amplifiers might be wise to slow down the bridge with modest values of resistance, rather than leave the damping to the unpredictable value of ESR in the first filter cap. This is probably the reason why adding a film bypass cap makes this type of supply sound worse; as a result of the film bypass decreasing the effective ESR, the current pulse is speeded up and EMI emission increased.
As can be imagined, this Tesla-coil-in-miniature is going to be very sensitive to physical layout, stray C's and R's in the power transformer, and stray L's and R's in the first capacitor. Slowing down the rectifier with ferrite beads might be a no-go as well, since the current pulse is very fast, very large, and can easily saturate the ferrite. Small values of resistance with inductive-type wirewounds, one on each leg of the bridge, are the best way to moderate the RF emission at the source. Not much chance of saturating something as inert as a wirewound resistor — and the residual inductance is an air-core, no saturation there either.
The distance between the power transformer, bridge, and first cap determines the loop area of the noise-source antenna, and the peak current pulse indicates the power this antenna is likely to emit. Something as simple as twisting the power supply lines with an associated ground return can reduce antenna emission by 20 dB. Noise suppression requires a combination of noise reduction at the source (any sub-circuit that switches rapidly) as well as RF-style shielding techniques.
Mainstream AES-school engineers have ridiculed "audiophile" power cords for many years, but EMI emission from solid-state-rectifier power supplies is no joke. It's hard to identify on a scope (the trace just looks a little thicker), but a wideband spectrum analyzer clearly displays the comb spectra created by the switching devices. The fancy power cords may be doing their greatest benefit by partially shielding the dirty power supplies from other solid-state equipment and CD players.
Of course, this begs the question: why tolerate dirty supplies at all? The broadband noise is radiated in all directions: into the circuit boards, the grounds, inside the chassis, and out the power cord. If any partly-filtered digital residue is floating around (and this is inevitable in even the costliest DAC's and CD players), the power supply noise will cross-modulate with digital residue as soon as the first nonlinear circuit element is encountered. How linear are most op-amps at 1 MHz? Not very. That's video-amp territory, not audio.
Every time you see a transformer, solid-state bridge, and input cap, you have a noise problem. Yes, HEXFREDs, Schottky diodes, and snubber circuits will help. But the problem of an extremely fast charging-current pulse remains, and is worsened by Class AB operation. (If you think preamps are exempt, think again. Very few opamps are Class A; most are Class AB, and many are quasi-complementary Class AB at that.) The application of inductors, shielded sub-enclosures, and RF noise suppression techniques to audio equipment is decades overdue. The only reason it has gone on so long is that few audio engineers (much less digital engineers) are familiar with RF technology, including routine use of wideband spectrum analyzers to "sniff" circuits for spurious emissions.
Closing Thoughts
This brief discussion of amplifiers is intended to point out how traditional measurements result in unwise decisions for amplifier design. The lower harmonics are nearly inaudible compared to the upper harmonics, yet they dominate almost any THD measurement! The meter is steering the designer, the reviewer, the dealer, and the consumer away from good sound.
It’s the classic tale of a drunk looking for his car keys under the street-light, even though he suspects he lost them in a completely different place. "The light is better here!" say the mainstream engineers, mass-marketers, and magazine reviewers — but the key to good sound sure isn’t where the audio industry has been looking.
If it were, why do stereo LP’s made 40 years ago, amplified with 65-year-old direct-heated triodes, sound so much better than today’s digital sound played through 0.001% THD mass-fi rack stereos? The differences between mass-fi and true high fidelity are as plain as day to an (open-minded) listener.
We are in the odd position of discovering that as speakers get better and better, the true merits of vacuum-tube circuits become more and more evident. After all, even J. Gordon Holt gave the Crown DC-300 transistor amplifier a Class "A" rating in 1971. At the time, the modestly-priced Dyna Stereo 70 received a lower rating - yet with modern speakers, the DC-300 is unlistenable, and the Dyna just keeps sounding better. The entry-level EL84 amps of the early Sixties (Scott 299, Eico, and Dyna SCA-35) sound remarkably natural and realistic with today’s more efficient, and much more transparent, speakers.
There is no reason to believe speakers will stop getting better, since all kinds of new innovations in materials science are on the horizon, and there are major advances in computer modelling techniques every year. Synthetic diamond cones, anyone?
It’s time to debunk the myth of "euphonic distortion" once and for all and discover the genuine and subtle sources of amplifier distortion that people are actually hearing. Once we find measurements that can actually help, rather than hinder, it'll be easier to build electronics that are friendly to the listener. I hope this article gets people thinking, and most important of all, listening for themselves!
Return to the Library
© Lynn Olson 1997, 2001, 2003. All Rights Reserved.
First published in "Glass Audio" magazine by Lynn Olson, revised in 2001 and 2003.